Standard Deviation (Topic 7.2)
This is going to be an interesting post due to the lack of caracters available to input to demonstrate the equation. I realise that S.D can be confusing anyway, but I will do my best here!
 |
| Standard Deviation Equation |
 |
| Key to the symbols used in the equation |
Do not be daunted! It's not as scary as it seems - honest!!
I will demonstrate 2 methods to calculate standard deviation, one in 6 steps, the second in 3 steps. Personally, I use the second method as it takes less time, but it is entirely up to you - the same result is achieved.
METHOD 1
Question: Calculate the standard deviation of the following data: 4, 1, 2, 3, 5, 0
- Calculate the mean [
]: 4 + 1 + 2 + 3 + 5 + 0 = 15 15 ÷ 6 =2.5
- Subtract mean from measure values [x -]: 4-2.5, 1-2.5, 2-2.5, 3-2.5, 5-2.5, 0-2.5
1.5 -1.5 -0.5 0.5 2.5 -2.5
- Square all the numbers [ (x - )² ]: 1.5² -1.5² -0.5² 0.5² 2.5² -2.5²
2.25 -2.25 -0.25 0.25 6.25 -6.25
- Add all squared numbers together [ ∑(x -)² ]: 2.25+2.25+0.25+0.25+6.25+6.25 = 17.5
Remember to cancel out all "-" and replace with "+" numbers - I find this confusing which is why I opt for Method 2.
- Divide answer by the total number of measurements minus one [ ∑(x -
)² / n-1 ]: 17.5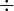 
5 = 2.917
- Square root ∑(x -)² 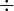measurements minus one: √ 17.5 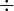5 = 1.87
METHOD 2
Question: Calculate the standard deviation of the following data: 4, 1, 2, 3, 5, 0
- Calculate mean []: 4 + 1 + 2 + 3 + 5 + 0 = 15 15 ÷ 6 =2.5
- Subtract mean from measure values [x -]: 4-2.5, 1-2.5, 2-2.5, 3-2.5, 5-2.5, 0-2.5
1.5 -1.5 -0.5 0.5 2.5 -2.5
- Square root÷ by number of measurements minus 1:
GOOD LUCK!! :)
No comments:
Post a Comment